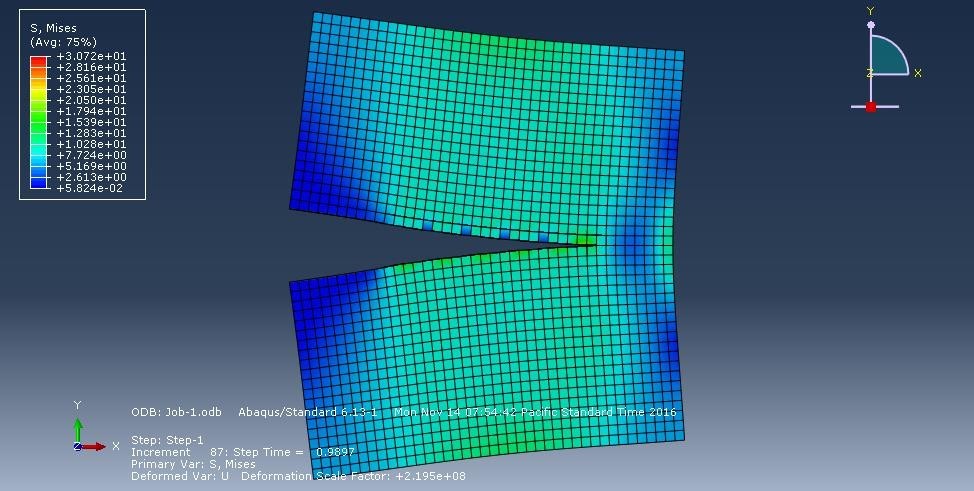
Crack propagation Analysis in a plate Using Abaqus

Crack propagation prediction helps engineers to optimize designs for enhanced durability and safety in real-world. In this post, we provides a step-by-step crack propagation analysis in a plate using Abaqus. The Extended Finite Element Method (XFEM) provides an efficient way to simulate crack growth without requiring frequent remeshing. This Feature making it ideal for modeling complex fracture behavior.

Problem definition for simulating crack in square plate

2D deformable shell (4 m × 4 m). With 1 m Crack length

Using XFEM within Abaqus, provides ability to simulate crack initiation and propagation under applied stresses and loads.

Whether you’re tackling fatigue analysis, structural integrity assessments, or damage tolerance studies, this guide provides suitable insights for fracture simulation and crack growth using XFEM.

You can Read about Crack propagation analysis here

You can Download Step-by-Step Crack propagation Analysis Abaqus CAE file for free

Pre Crack Analysis Setup in Abaqus

Material Properties (Aluminum)

• Young’s Modulus: 70 GPa
• Poisson’s Ratio: 0.33
• Density: 2700 kg/m³ (optional for static analysis)
• Damage Initiation:
  • Criterion: Maximum Principal Stress (MAXPS = 250 MPa, typical for aluminum).
• Damage Evolution:
  • Type: Displacement-based softening.
  • Displacement at Failure: 0.1 m (user-defined).

Abaqus Workflow for Crack Modeling

Step 1: Geometry & Assembly

1. Part: Create a 2D deformable shell (4 m × 4 m).
2. Crack: Define the initial crack as a partition (1 m long).
3. Assembly: Position the plate in the global coordinate system.

Step 2: Material Assignment

– Defining Material Properties for crack propagation Analysis

To create material properties, enter the Property module, double-click on Material in the tree view, and proceed as follows.

Name: Aluminum, Mechanical:

Elasticity → Young’s Module: 70 × 10⁹ ,Poisson’s Ratio: 0.33 → ok Elasticity → Damage for Traction Seperation Laws → Maxps Damage: 10

Click on the Damage Evolution suboption and enter a value of 0.1 for the change in position at the moment of damage. Then click OK twice to close the material Edit window.

Step 3: Loads & Boundary Conditions for Crack propagation

1. Pressure Load: Apply -5.5 MPa to the top edge.
2. Boundary Conditions:
   • Bottom Edge: Fully fixed (U1=U2=UR3=0).
   • Sides: Allow vertical displacement only (U1=0).

Step 4: XFEM Crack Definition in Abaqus

1. Interaction Module:
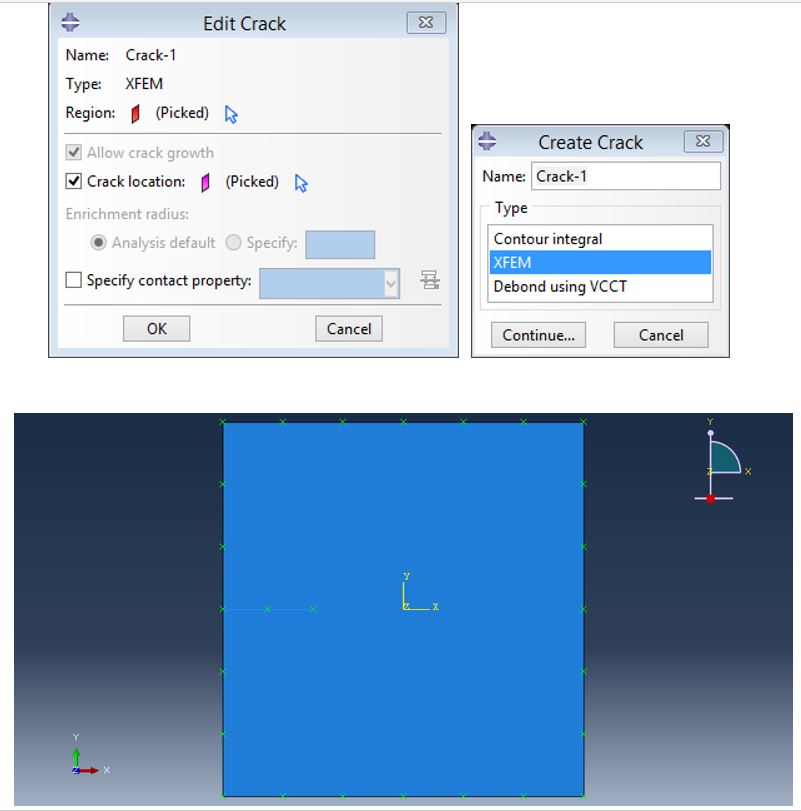
   • Go to Special > Crack > Create.
   • Type: XFEM.
   • Crack Domain: Select the plate.
   • Enrichment Radius: 0.1 m (adjust based on mesh size).
   • Initial Crack: Select the partitioned crack line.

Defining the contact between crack and geometry

Enter the Interaction environment and select special from the top menu and then crack and click on create to open the following window. In this window, select XFEM and continue. Select the square and in the opened window, check the location crack to activate the flash icon. Click on this icon and select the crack and then Done and then ok.

Step-5: Creating Geometry in Abaqus for Crack propagation analysis

To draw a track, enter the Part module and proceed as follows:

Create Part  → Modeling Space: 2D, Type: Deformable, Base Feature: wire, Type: Planar, Approximate size: 2→ Continue

Click on the wire and enter the following coordinates. Then click the cross at the bottom of the page and Done.

(-2,0), (-1,0)

Step 6: Meshing

1. Mesh Module:
   • Use quad-dominated elements (e.g., CPS4R for plane stress).
   • Refine mesh near the crack tip (element size ≈ 0.1 m).
   • Click on Seed Part Instance and enter  0.1 for Approximate Global Size

Step 6: Analysis Step and Job Submission

1. Static, General Step:
   • Enable Nonlinear Geometry (for large deformations).
   • Incrementation: Set initial/minimum/maximum increments (e.g., 0.01, 1e-5, 0.1).
   • Field Outputs: Request STATUSXFEM, S, E, DAMAGEC, DAMAGET.

for job submission Specify the path to save the file and then click the Submit option to start solving the problem.