Abaqus Material Models Under Different Loading Conditions

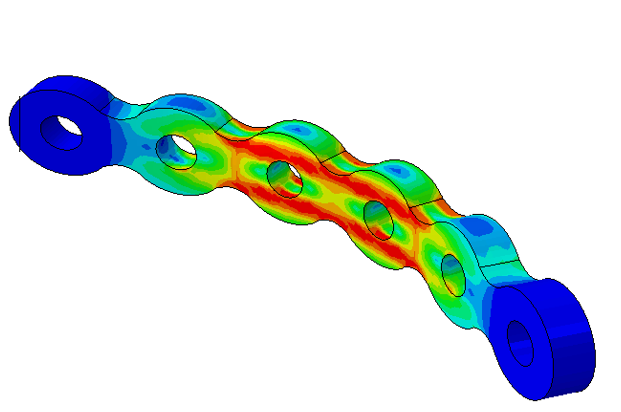
Material modeling is a fundamental aspect of computational simulations in engineering and material science. Understanding how different materials behave under various loading conditions allows engineers to predict failure, optimize design, and improve product performance. This article provides an overview of various material models, their behavior under different loading conditions, examples of each material type, and how these models are implemented in Abaqus.

Various Material Models in Abaqus

Material models describe the relationship between stress and strain for a given material. The most common types include:

1. Elastic Models

Elastic behavior in materials refers to the ability of a material to return to its original state after being subjected to a force or stress that causes it to deform. This occurs when the applied stress does not exceed the material’s elastic limit, that is, the maximum amount of stress a material can withstand without undergoing permanent deformation.

They follow Hooke’s law, which states that stress is proportional to strain up to the elastic limit.

Linear Elastic Model

• Assumes a linear relationship between stress and strain.
• Defined by Young’s modulus (E) and Poisson’s ratio (ν).
• Example materials: Steel, Aluminum, Glass.

Nonlinear Elastic Model

• The relationship between stress and strain is nonlinear but fully recoverable.
• Example materials: Rubber-like polymers, biological tissues.

2. Plastic Models

is a property of materials that allows for permanent changes in their shape when subjected to stress. This behavior is observed in a wide range of materials, including metals, rocks, concrete, foams, and soils.

Elastic-Plastic Model

• Includes an elastic region followed by a plastic deformation phase.
• Requires a yield criterion, such as von Mises or Tresca.
• Example materials: Mild Steel, Copper, Brass.

Strain-Hardening Plasticity

• Accounts for an increase in strength with plastic deformation.
• Example materials: Cold-worked metals, High-strength alloys.

3. Viscoelastic Models

Viscoelastic materials exhibit both viscous (fluid-like, time-dependent) and elastic (solid-like, instantaneous) behavior. Viscoelastic models mathematically describe how these materials respond to mechanical loads over time, capturing phenomena such as creep, stress relaxation, and hysteresis.

Examples of Viscoelastic Materials:

• Polymers: Rubber, silicone, PVC, PMMA (acrylic).
• Biological tissues: Cartilage, tendons.
• Adhesives and gels.

4. Viscoplastic Models

Viscoplastic materials exhibit time-dependent plastic deformation.

Theory: Combines elastic and viscous behavior (time-dependent response).
Behavior:

• Creep: Deformation under constant load.
• Stress Relaxation: Stress reduction under constant strain.
  Examples:
• Polymers (e.g., PVC, PMMA).
• Biological materials (e.g., cartilage).

• Example materials: Lead, High-temperature alloys, Soft metals under high strain rates.

5. Hyperelastic Models

Hyperelastic models describe the nonlinear elastic behavior of materials that undergo large deformations, such as rubber, elastomers, and soft tissues. Unlike linear elasticity (Hooke’s Law), hyperelasticity assumes a strain energy function ($W$) that relates stress to strain, capturing phenomena like:

• Large strains: Up to 100% or more.
• Incompressibility: Near-zero volume change.
• Nonlinear stress-strain curves: Stiffening or softening under deformation.

Examples of Hyperelastic Materials:

• Rubber (e.g., neoprene, silicone).
• Biological tissues (e.g., skin, arteries).
• Soft polymers (e.g., polyurethane, PDMS).

6. Creep Models

Creep failure occurs in a material when it is subjected to constant load over prolonged periods of time. This is permanent deformation occurring in the material due its inherent atomic or molecular structure. This failure occurs when the stresses are well below the yield stress of the material.

Creep models describe the time-dependent deformation of materials under constant stress, typically at elevated temperatures. Creep is characterized by three stages:

1. Primary Creep: Rapid initial deformation with decreasing strain rate.
2. Secondary Creep: Steady-state deformation with constant strain rate.
3. Tertiary Creep: Accelerated deformation leading to failure.

Creep is critical in industries like aerospace, power generation, and automotive, where components operate under high stress and temperature for extended periods.

Examples of Materials Exhibiting Creep:

• Metals: Steel, aluminum, titanium (at high temperatures).
• Polymers: PVC, polyethylene.
• Ceramics: Concrete, glass.

Read this for more about Creep Models 

Key Creep Behaviors

1. Time-Dependent Strain:
   • Strain increases over time under constant stress.
2. Temperature Dependence:
   • Creep rates increase exponentially with temperature.
3. Stress Dependence:
   • Higher stress leads to faster creep deformation.
   
   How to do Fatigue life prediction in Abaqus?
   

    

   7. Damage and Failure Models in Abaqus

   These models describe material degradation and failure due to cracks, fatigue, or other mechanisms.

   Progressive damage and failure in materials refers to the process where a material gradually loses its load-carrying capacity due to the degradation of its stiffness. This process is typically modeled using damage mechanics.

   Abaqus offers a rich set of features to predict and analyze progressive damage and failure in various types of materials. This includes a general framework for material failure modeling that allows for multiple simultaneous failure mechanisms and is designed to alleviate mesh dependency.

   • Cohesive Zone Model: Describes crack propagation.
   • Ductile Damage Model: Predicts failure in metals.
   • Example materials: Composite materials, Ceramics, Structural metals.

   Read more about Damage and Failure Models in Abaqus

   

    Effect of Loading Conditions on materials behavior

   1. Tensile Loading

   • Metals exhibit elastic behavior followed by yielding and strain hardening.
   • Polymers show necking and may fail by crazing or shear yielding.
   • Ceramics often fail catastrophically without yielding.

   2. Compressive Loading

   • Ductile metals deform plastically.
   • Brittle materials like ceramics fracture suddenly.
   • Polymers may exhibit buckling or yielding.

   3. Shear Loading

   • Metals undergo slip and plastic deformation.
   • Polymers exhibit shear yielding.
   • Ceramics show limited shear strength before fracture.

   4. Cyclic Loading (Fatigue)

   • Metals may experience fatigue failure after repeated stress cycles.
   • Polymers degrade due to molecular chain scission.
   • Ceramics have low fatigue resistance due to crack growth.
   • Click here for Models for metals subjected to cyclic loading

   5. High-Temperature Loading

   • Metals experience creep deformation.
   • Polymers soften or degrade.
   • Ceramics can withstand high temperatures but may experience thermal shock failure.

   Material Models Used in Abaqus

   Abaqus provides a variety of material models to capture different material behaviors, including:

   1. Elastic Models

   • Linear Elasticity: Defined using Young’s modulus and Poisson’s ratio.
   • Hyperelasticity: Models like Neo-Hookean, Mooney-Rivlin, and Ogden for rubber-like materials.

   2. Plasticity Models

   • Elastic-Plastic: Includes isotropic and kinematic hardening.
   • Johnson-Cook: Used for high strain rate applications.
   • Drucker-Prager: For granular materials like soil and concrete.

   3. Viscoelastic Models

   • Time-dependent behavior: Prony series is used to define relaxation behavior.

   4. Creep and Viscoplastic Models

   • Norton’s Law: Describes time-dependent creep behavior.
   • Power Law: Used for long-term deformation studies.

   5. Damage and Failure Models

   • Ductile Damage: Used for metals.
   • Cohesive Zone Model: Used for fracture simulations in composites.
   • XFEM (Extended Finite Element Method): Simulates crack growth without remeshing.

   How to Use These Models in Abaqus

   1. Defining a Material Model

   1. Open Abaqus/CAE and create a new material in the Property module.
   2. Select the appropriate material model (Elastic, Plastic, Viscoelastic, etc.).
   3. Input material parameters (e.g., Young’s modulus, Poisson’s ratio for elasticity).
   4. For advanced materials, define behavior using tables or user subroutines (UMAT/VUMAT).

   2. Assigning the Material to a Part

   1. Create a section and assign the material.
   2. Assign the section to the part.
   3. Verify material assignments in the visualization module.

   3. Running the Simulation

   1. Apply boundary conditions and loading conditions.
   2. Choose an appropriate solver (Static, Dynamic, Explicit).
   3. Run the simulation and analyze results using stress-strain plots.

   4. Advanced Features

   • Use subroutines (UMAT/VUMAT) for custom material behavior.
   • Implement user-defined creep models for long-term simulations.
   • Define failure criteria for fracture mechanics studies.

   Conclusion

   The article emphasizes the importance of selecting the appropriate material model in Abaqus to achieve accurate and reliable finite element analysis (FEM). Material models in Abaqus are crucial for effectively predicting real-world material behaviors, including elasticity, plasticity, and failure. With the wide variety of materials and loading conditions in engineering applications, choosing the right model is fundamental to ensuring precise and dependable simulation results.