Understanding the effects of linear and non-linear material properties is crucial for accurate simulations in finite element analysis (FEA) in Abaqus or etc. Below is a structured comparison, highlighting their differences in behavior, computational demands, applications, and implications for engineering design. In this simulation with Abaqus software, fundamental understanding of the This tutorial compares the effects of linear and non-linear material properties is assumed.
Linear Material Properties:
- Follow Hooke’s Law () with a proportional stress-strain relationship.
- Assumes small deformations and reversible elasticity (no permanent deformation).
- Examples: Metals in the elastic regime, glass, ceramics.
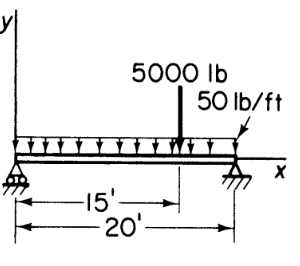
Create a material with the following properties in Abaqus; Name: Steel_Linear Modulus: 210 GPa , Poisson’s: 0.3
Non-Linear Material Properties in Abaqus:
- Stress-strain relationship is not proportional; includes plasticity, hyperelasticity, viscoelasticity, or creep.
- Accounts for irreversible deformation, time-dependence, or large-strain behavior.
- Examples: Ductile metals (plasticity), rubber (hyperelasticity), polymers (viscoelasticity).
To model the plastic behaviour we need to define some plastic material properties. These are input as a Yield Stress – Plastic Strain table and are interpolated between the defined values but no curve fit is used. It is important to note that Abaqus uses true stress-strain values rather than Engineering stress-strain as the material model does not account for necking Create a new material and define the following Elastic properties in Abaqus; Name: Steel_Nonlinear Modulus: 210 GPa Poisson’s: 0.3 Create Plastic definition and enter the following values; Yield Stress 300 310 Plastic Strain 0 0.1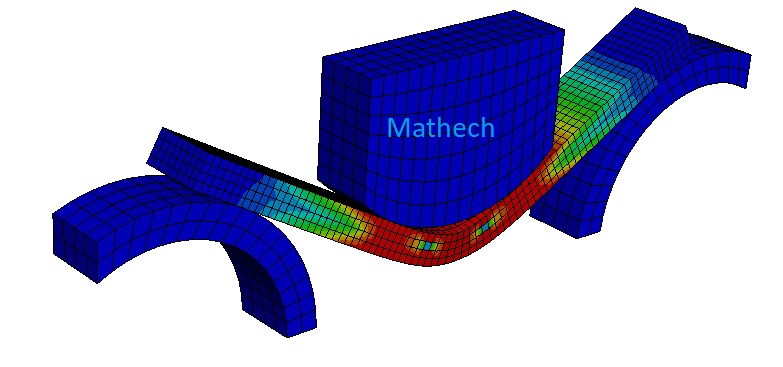 
Stress-Strain Behavior
| Aspect | Linear Materials | Non-Linear Materials |
|---|---|---|
| Stress-Strain Curve | Straight line (elastic region only). | Curved or path-dependent (e.g., plasticity, hyperelasticity). |
| Permanent Deformation | None (fully reversible). | Possible (e.g., plasticity). |
| Yield Point | No yielding; failure at ultimate strength. | Defined yield stress (σy) with post-yield hardening/softening. |
| Time Dependency | None. | Present in viscoelasticity, creep, or relaxation. |
Read more about Difference between linear and nonlinear elastic material Read more about Various Material Models in Abaqus
Computational Requirements
| Aspect | Linear Materials | Non-Linear Materials |
|---|---|---|
| Solver Type | Linear solvers (fast, direct methods). | Non-linear solvers (iterative, incremental methods). |
| Convergence | Guaranteed (no iterations needed). | May require small time steps, adaptive meshing, and stabilization. |
| Computational Cost | Low (suitable for quick design checks). | High (demands more memory and processing power). |
Applications
- Linear Materials:
- Use Cases: Static analyses of structures under service loads (e.g., bridges, buildings), stiffness checks, modal analysis.
- Limitations: Inaccurate for predicting failure, large deformations, or ductile behavior.
- Non-Linear Materials:
- Use Cases:
- Plasticity: Crash simulations, metal forming, ductile failure analysis.
- Hyperelasticity: Rubber seals, tires, biomaterials.
- Viscoelasticity/Creep: Polymers, asphalt, high-temperature components.
- Strengths: Captures real-world phenomena like energy dissipation, progressive failure, and time-dependent deformation.
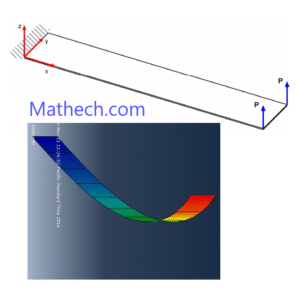
- Non-Linear Static Stress Analysis
- Non-linear buckling and post-buckling behaviour analysis
- Non-Linear Dynamic Analysis
- Non-linear Modal analysis
- Frequency response using harmonic balance method
- Full transient analysis
- Use Cases:
Impact on Simulation Results
- Linear Analysis:
- Predicts linear deflection and stress distribution.
- Overestimates load-bearing capacity beyond yield (risk of unsafe designs).
- Misses failure modes like buckling post-yield or plastic collapse.
- Non-Linear Analysis:
- Captures permanent deformation (e.g., crumple zones in cars).
- Models path-dependent behavior (e.g., residual stresses after forming).
- Predicts progressive failure (e.g., necking in metals).
Practical Examples
- Car Bumper Impact:
- Linear: Underestimates energy absorption; predicts unrealistic elastic rebound.
- Non-Linear (Plasticity): Shows permanent deformation and realistic energy dissipation.
- Rubber Gasket Compression:
- Linear: Fails to model large-strain hyperelastic behavior.
- Non-Linear (Hyperelasticity): Accurately predicts non-linear stress-strain curves and sealing performance.
- Bridge Collapse Analysis:
- Linear: Predicts sudden failure at ultimate load.
- Non-Linear (Plasticity): Reveals plastic hinge formation and collapse mechanism.
Learning Objectives of this simulation in Abaqus
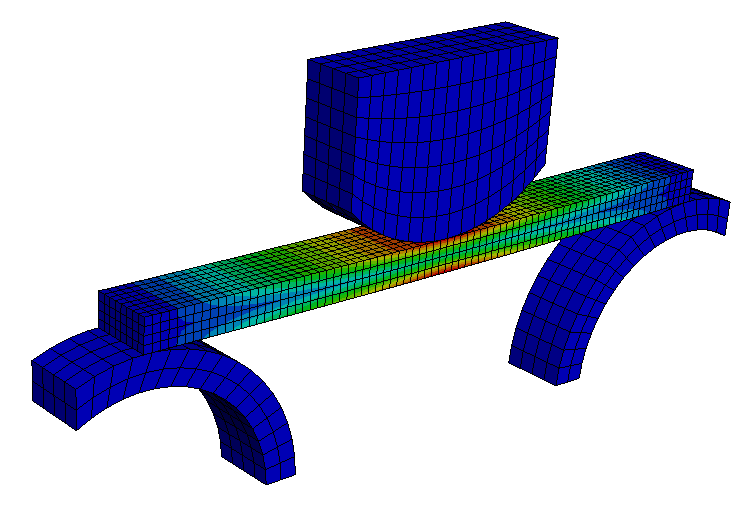
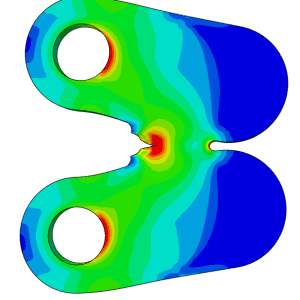
• Investigate the effects of plasticity o Include plastic material properties o Compare an elastic/plastic model to elastic only • Exploit the symmetry within a model • Apply a displacement • Visualize results for more than one model at once o Stack Viewports o Link Viewports In this tutorial we will be comparing Linear and Non-Linear material properties. First we will create the Linear material properties as we have previously then add in the Non-Linear properties later in the tutorial. 
What do you notice about the difference between the two models in Abaqus? The only difference between the two models is that one includes plastic material properties, however they give completely different answers. Both contained the same loads, boundary conditions, interaction etc. and both obtained a converged solution without a problem. Individually it may look like both are correct but side-by-side it is clear that one is wrong.
Reviews
There are no reviews yet.