Damage Types in Abaqus

One of Abaqus key strengths lies in its robust damage modeling capabilities, which allow engineers to predict material failure and degradation accurately. This article provides an in-depth exploration of damage types in Abaqus, categorized by material and application, including ductile metals, traction-separation laws, fiber-reinforced composites, and elastomers. Each damage type is defined, and its applications are discussed to help engineers and researchers leverage Abaqus effectively.

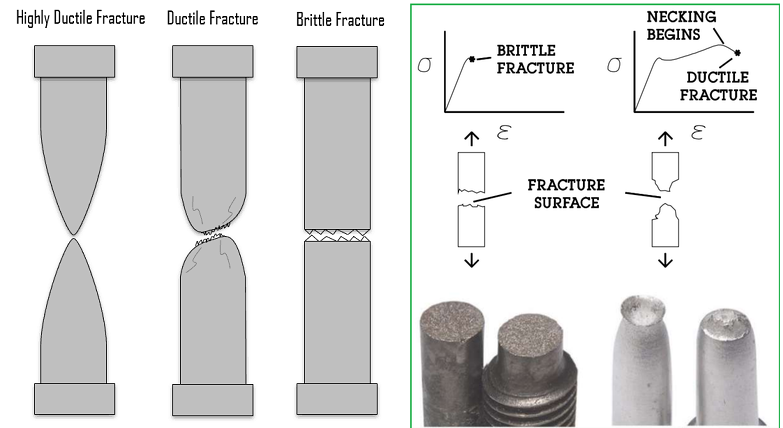
Brittle and Ductile Fracture

Damage Types for Ductile Metals in Abaqus

Ductile metals, such as steel, aluminum, and copper, undergo significant plastic deformation before failure. Abaqus provides several damage models to capture their failure mechanisms under various loading conditions. Below are the primary damage types for ductile metals, their definitions, and applications.

1.1 Ductile Damage

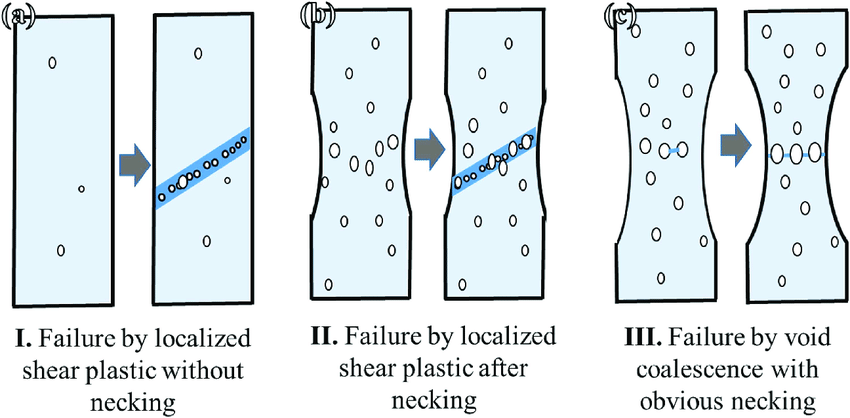
Definition: Ductile damage models the failure of ductile metals due to void nucleation, growth, and coalescence under tensile or compressive loading. It uses a damage initiation criterion based on equivalent plastic strain and stress triaxiality, followed by damage evolution that reduces material stiffness until element deletion. Applications:

• Crashworthiness analysis in automotive structures (e.g., car frames).
• Metal forming processes (e.g., deep drawing, forging).
• Structural components under high plastic deformation (e.g., pipelines, pressure vessels).

1.2 Johnson-Cook Damage

Definition: The Johnson-Cook damage model is a temperature- and strain-rate-dependent model for ductile metals, combining plasticity and damage. It defines damage initiation based on a cumulative damage parameter influenced by strain rate, temperature, and stress triaxiality, with damage evolution leading to fracture. Applications:

• High-speed impact simulations (e.g., ballistic impacts on armor).
• Machining processes (e.g., cutting, drilling).
• Aerospace components under dynamic loading (e.g., turbine blades).

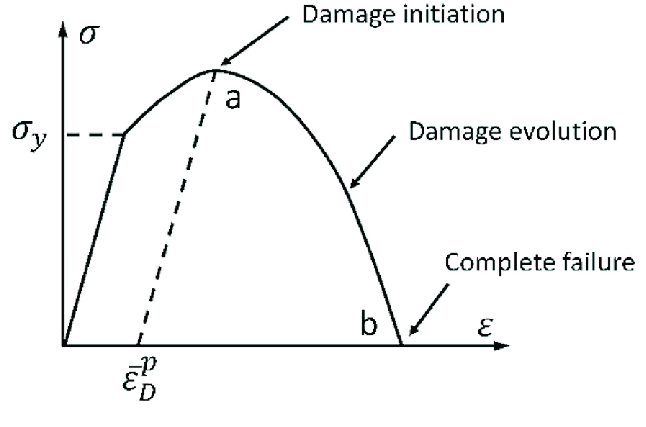
1.3 Shear Damage

Definition: Shear damage targets failure in ductile metals under shear-dominated loading. It uses a shear strain-based criterion for damage initiation, often combined with ductile damage, and accounts for shear band formation and material degradation. Applications:

• Shear failure in bolted or riveted joints (e.g., aerospace assemblies).
• Machining processes involving shear-dominated deformation.
• Thin-walled structures under shear loading (e.g., aircraft skins).

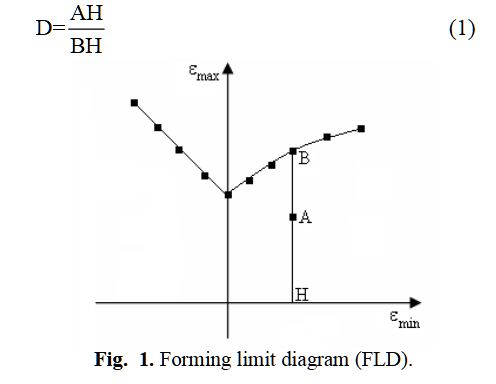
1.4 FLD Damage (Forming Limit Diagram Damage)

Definition: FLD damage predicts necking and failure in sheet metals during forming processes. It uses a forming limit diagram, which defines critical major and minor strain combinations, to initiate damage when strains exceed the limit curve. Applications:

• Sheet metal forming (e.g., stamping, stretch forming).
• Automotive body panel manufacturing.
• Prediction of localized necking in thin metal sheets.

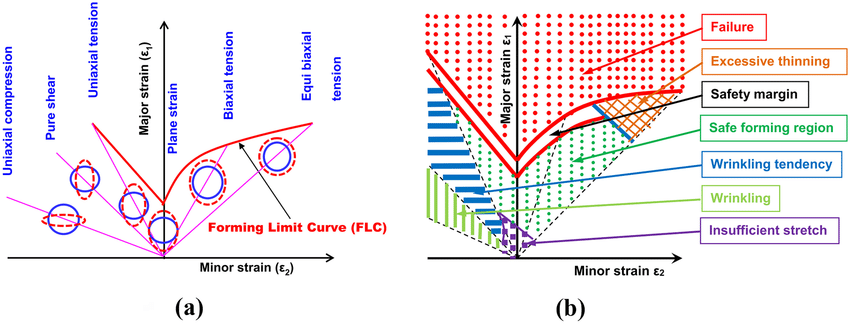
1.5 FLSD Damage (Forming Limit Stress Diagram Damage)

Definition: FLSD damage extends the FLD approach by using a stress-based forming limit criterion, which is path-independent and accounts for complex loading histories. It is particularly useful for multi-stage forming processes. Applications:

• Multi-stage sheet metal forming (e.g., deep drawing with multiple steps).
• Automotive and aerospace sheet metal components.
• Processes with non-proportional loading paths.

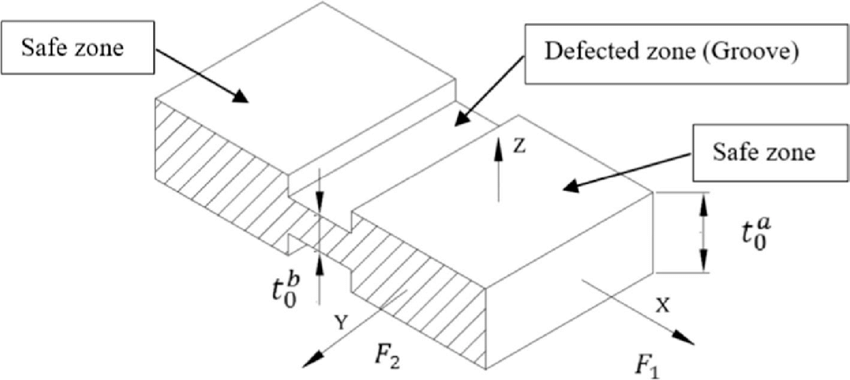
1.6 M-K Damage (Marciniak-Kuczynski Damage)

Definition: The Marciniak-Kuczynski (M-K) model predicts localized necking in sheet metals by assuming an initial imperfection (e.g., a groove) in the material. Damage initiates when the strain in the imperfection region reaches a critical value, leading to necking and failure. Applications:

• Sheet metal forming simulations requiring high accuracy in necking prediction.
• Automotive and appliance manufacturing (e.g., car hoods, refrigerator panels).
• Research on material formability limits.

1.7 MSFLD Damage (Modified Stress-Based Forming Limit Diagram Damage)

Definition: MSFLD damage is a modified version of FLSD, incorporating additional factors like strain path effects and material anisotropy. It provides a more robust stress-based criterion for predicting failure in complex forming processes. Applications:

• • Advanced sheet metal forming with anisotropic materials.
  • Aerospace components with complex geometries.
  • Simulations requiring high-fidelity failure prediction under varying strain paths.

Damage Types for Traction-Separation Laws in Abaqus

Traction-separation laws are used in Abaqus to model cohesive behavior, such as adhesive bonding, delamination, or crack propagation in cohesive elements or surfaces. These models define damage initiation and evolution based on traction (stress) and separation (displacement) across an interface. Below are the key damage types for traction-separation laws.

2.1 Quade Damage (Quadratic Nominal Stress Criterion for Damage Initiation)

Definition: Quade damage initiates when a quadratic function of nominal stress ratios (normal and shear stresses) reaches a critical value. It is used to model mixed-mode failure in cohesive interfaces. Applications:

• Adhesive bonding in composite structures (e.g., bonded aircraft panels).
• Delamination in laminated composites.
• Fracture in brittle coatings.

2.2 Maxe Damage (Maximum Nominal Stress Criterion for Damage Initiation)

Definition: Maxe damage initiates when the maximum nominal stress (normal or shear) exceeds a critical value. It is simpler than Quade and suitable for cases dominated by a single mode of failure. Applications:

• Single-mode delamination in composites (e.g., Mode I opening).
• Adhesive failure in simple bonded joints.
• Crack initiation in thin films.

2.3 Quads Damage (Quadratic Nominal Strain Criterion for Damage Initiation)

Definition: Quads damage uses a quadratic function of nominal strain ratios to initiate damage, focusing on strain-based failure in cohesive interfaces. It is useful for materials with significant deformation before failure. Applications:

• Delamination in flexible composites or polymers.
• Adhesive joints with large deformations.
• Soft material interfaces (e.g., bio-adhesives).

2.4 Maxs Damage (Maximum Nominal Strain Criterion for Damage Initiation)

Definition: Maxs damage initiates when the maximum nominal strain (normal or shear) exceeds a critical threshold. It is analogous to Maxe but strain-based, suitable for ductile interfaces. Applications:

• Ductile adhesive failure in automotive assemblies.
• Cohesive failure in soft composites.
• Interfaces with significant plastic deformation.

2.5 Maxpe Damage (Maximum Principal Stress Criterion for Damage Initiation)

Definition: Maxpe damage initiates when the maximum principal stress in the cohesive interface exceeds a critical value. It is effective for brittle interfaces where principal stresses drive failure. Applications:

• Brittle adhesive failure in aerospace structures.
• Crack propagation in ceramic coatings.
• Delamination in high-stiffness composites.

2.6 Maxps Damage (Maximum Principal Strain Criterion for Damage Initiation)

Definition: Maxps damage initiates when the maximum principal strain exceeds a critical threshold. It is used for interfaces where strain-based failure dominates, particularly in ductile or flexible materials. Applications:

• Flexible adhesive joints in automotive or marine applications.
• Delamination in polymer-matrix composites.
• Interfaces in soft or elastomeric materials.

Damage for Fiber-Reinforced Composites: Hashin Damage

Definition: The Hashin damage model is designed for fiber-reinforced composites, capturing four primary failure modes: fiber tension, fiber compression, matrix tension, and matrix compression. It uses stress-based criteria to initiate damage and a degradation law to reduce stiffness in damaged regions. The model accounts for the anisotropic nature of composites and is widely used for laminated structures. Applications:

• Aerospace components (e.g., aircraft wings, fuselage panels).
• Wind turbine blades made of glass or carbon-fiber composites.
• Automotive composite structures (e.g., carbon-fiber chassis, crash structures).
• Sporting goods (e.g., composite bicycle frames, tennis rackets).

4. Damage for Elastomers: Mullins Effect

Definition: The Mullins effect models the stress-softening behavior in elastomers (e.g., rubber) under cyclic loading. It captures the reduction in stiffness after the first loading cycle due to microstructural changes, such as chain breakage or filler detachment. In Abaqus, it is implemented as a phenomenological model with parameters calibrated from experimental data. Applications:

• Rubber seals and gaskets in automotive and industrial applications.
• Tire design and performance analysis.
• Flexible medical devices (e.g., catheters, implants).
• Vibration dampers and shock absorbers.

Practical Considerations for Damage Modeling in Abaqus

1. Material Calibration: All damage models require accurate material parameters, which must be calibrated using experimental data (e.g., tensile tests, shear tests, or cyclic loading data). For ductile metals, obtain fracture strains and stress triaxiality; for composites, use fiber and matrix strengths; for elastomers, calibrate Mullins effect parameters from cyclic tests.
2. Mesh Sensitivity: Damage models, particularly for ductile metals and cohesive elements, are mesh-dependent. Use refined meshes in critical regions and consider techniques like element deletion, viscous regularization, or adaptive meshing to improve convergence and accuracy.
3. Computational Cost: Complex damage models (e.g., Hashin, Johnson-Cook) can be computationally intensive, especially for large-scale models. Choose explicit solvers for dynamic problems (e.g., impact, crash) and implicit solvers for quasi-static problems to balance efficiency and accuracy.
4. Validation: Validate simulation results against experimental or real-world data to ensure reliability. For example, compare predicted necking in FLD simulations with forming limit tests or validate Hashin damage predictions with composite coupon tests.
5. Model Selection: Select the appropriate damage model based on the material, loading condition, and failure mechanism. For instance, use Johnson-Cook for high-rate loading, Hashin for composites, and traction-separation laws for interface failure.

Conclusion

Abaqus offers a comprehensive suite of damage models tailored to various materials and applications, from ductile metals to composites, cohesive interfaces, and elastomers. By understanding the definitions and applications of these damage types—such as ductile damage, Johnson-Cook, Hashin, and the Mullins effect—engineers can accurately predict material failure, optimize designs, and enhance structural performance. Whether simulating automotive crashworthiness, aerospace composites, adhesive joints, or rubber components, Abaqus’s damage modeling capabilities provide the tools needed to tackle complex engineering challenges. To deepen your expertise, experiment with these damage models in Abaqus using realistic material data and loading conditions. For further guidance, refer to Abaqus documentation or consult with FEA experts to ensure accurate and reliable simulations. This article is designed to be detailed, technically accurate, and accessible for your website audience, including engineers, researchers, and students working with Abaqus. If you need specific examples for each damage type, formatting adjustments, or additional sections, please let me know!