Viscoelastic Material Modeling in Abaqus; Time Domain vs. Frequency Domain

Viscoelasticity is the property of a material that exhibits both viscous and elastic behavior when deformed. Synthetic polymers, wood, and human tissue, along with metals at high temperature, exhibit significant viscoelastic effects.

Abaqus provides some tools to model viscoelastic behavior in both the time and frequency domains.

📌 What Is Viscoelasticity?

Viscoelasticity is a material property that combines elastic (solid-like) and viscous (fluid-like) behavior.

viscoelastic materials exhibit time-dependent deformation under load and gradual recovery after unloading.

Key Characteristics of  Viscoelastic Materials

1. Time-Dependent Response

• Creep: Deformation increases under constant stress (e.g., rubber stretching over time).
• Stress Relaxation: Stress decreases under constant strain (e.g., tightened bolt losing tension slowly).

1. Strain-Rate Sensitivity
   • Stiffer under fast loading (impact), softer under slow loading (static load).
2. Hysteresis (Energy Dissipation)

• Stress-strain curves form loops during cyclic loading, indicating damping (e.g., car tires absorbing vibrations).

1. Memory Effect

• The material “remembers” past deformations (e.g., polymer slowly returning to its original shape).

Examples of Viscoelastic Materials

• Polymers: Rubber, plastics, adhesives.
• Biological Tissues: Cartilage, tendons, skin.
• Geomaterials: Asphalt, soft soils.
• Industrial Materials: Foams, gels, viscoelastic dampers.

 Mathematical Representation

Viscoelastic behavior is modeled using:

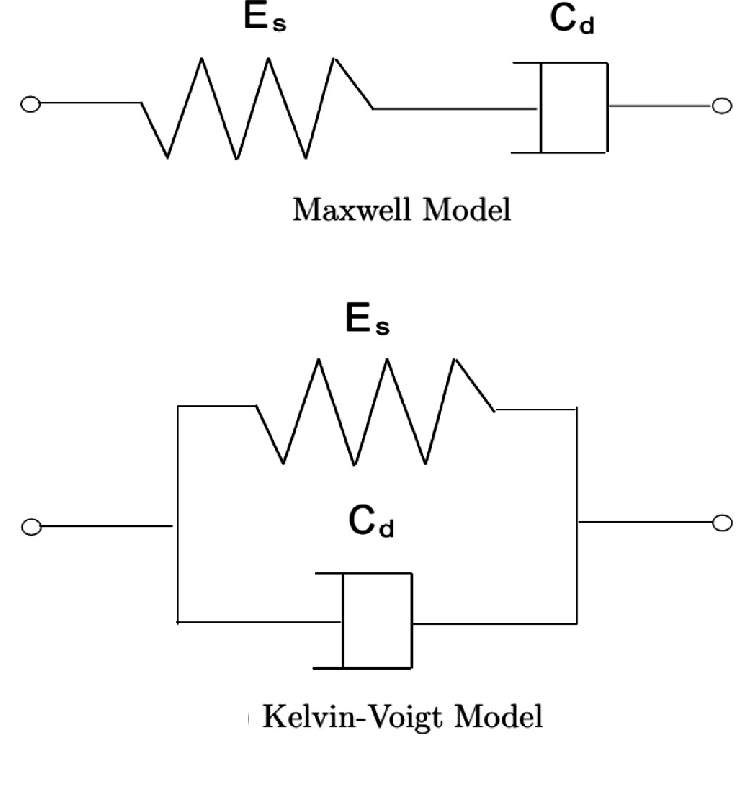
1. Spring-Dashpot Models
   • Maxwell Model (Spring + Dashpot in series) → Good for stress relaxation.
   • Kelvin-Voigt Model (Spring + Dashpot in parallel) → Good for creep.
   • Generalized Models (Prony series) → Captures multiple relaxation times.

1. Complex Modulus (Frequency Domain)
   • Storage Modulus (G”) → Elastic stiffness.
   • Loss Modulus (G”) → Viscous damping.
   • Loss Tangent (tan δ = G”/G’) → Measures damping efficiency.

🔹 Viscoelasticity in Abaqus

Abaqus supports viscoelastic modeling in:

1. Time Domain (Transient analysis) → Prony series for creep/relaxation.
2. Frequency Domain (Harmonic analysis) → Complex modulus for vibrations.

🛠️ Time Domain Viscoelasticity in Abaqus

This type of material model describes the isotropic rate-dependent behavior of materials for which the dissipative losses caused by internal damping effects must be modeled in the time domain.

Abaqus assumes that the time domain viscoelasticity is defined by a Prony series expansion. You can specify the Prony series parameters directly for each term in the Prony series. Alternatively, Abaqus can calculate the terms in the Prony series using time-dependent creep test data, time-dependent relaxation test data, or frequency-dependent cyclic test data that you provide.

Prony Series Expansion in viscoelastic material

Represents relaxation modulus as a sum of exponential decays:

where:

• G∞​ = Long-term shear modulus

• Gi​ = Prony coefficients

• τi​ = Relaxation times

Assumptions for the time domain viscoelastic material model:

• assumes that the shear (deviatoric) and volumetric behaviors are independent in multiaxial stress states (except when used for an elastomeric foam);
• can be used only in conjunction with Linear Elastic Behavior, Hyperelastic Behavior of Rubberlike Materials, or Hyperelastic Behavior in Elastomeric Foams to define the continuum elastic material properties;
• can be used in Abaqus/Explicit with Linear Elastic Traction-Separation Behavior;
• is active only during a transient static analysis (Quasi-Static Analysis), a transient implicit dynamic analysis (Implicit Dynamic Analysis Using Direct Integration), an explicit dynamic analysis (Explicit Dynamic Analysis), a steady-state transport analysis (Steady-State Transport Analysis), a fully coupled temperature-displacement analysis (Fully Coupled Thermal-Stress Analysis), a fully coupled thermal-electrical-structural analysis (Fully Coupled Thermal-Electrical-Structural Analysis), or a transient (consolidation) coupled pore fluid diffusion and stress analysis (Coupled Pore Fluid Diffusion and Stress Analysis);
• can be used in large-strain problems;
• can be calibrated using time-dependent creep test data, time-dependent relaxation test data, or frequency-dependent cyclic test data; and
• can be used to couple viscous dissipation with the temperature field in a fully coupled temperature-displacement analysis (Fully Coupled Thermal-Stress Analysis) or a fully coupled thermal-electrical-structural analysis (Fully Coupled Thermal-Electrical-Structural Analysis).

Frequency Domain Modeling for Viscoelastic Material

Frequency domain modeling in Abaqus is used to analyze the dynamic response of viscoelastic materials under harmonic (sinusoidal) loading.

The dissipative part of the material behavior is defined by giving the real and imaginary parts of g∗g* and k∗k* (for compressible materials) as functions of frequency.

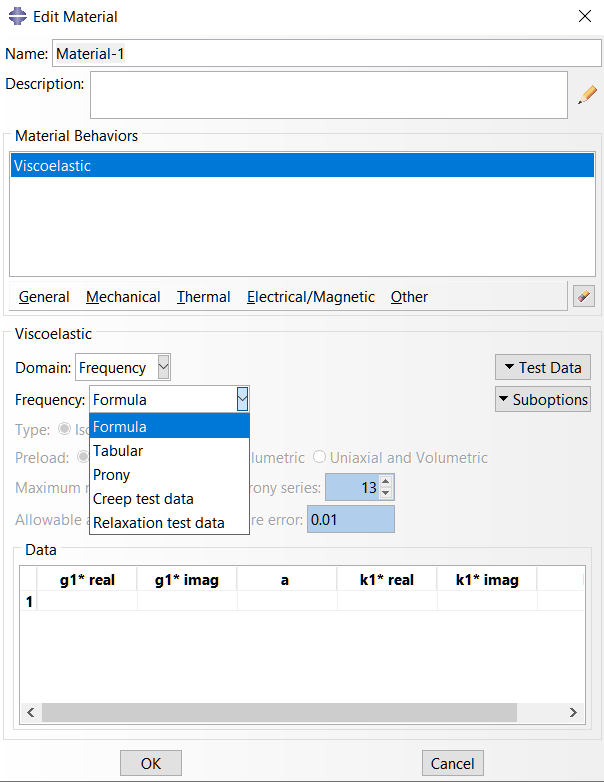
In the arrow to the right of the Frequency, you can select the option of your choice for determining viscoelastic material parameters:

• Select Formula to define the frequency dependence by the power law formulae.
• Select Tabular to define the frequency response in tabular form. You must provide the real and imaginary parts of
  ωg∗ and ωk∗ —where ω is the circular frequency—as functions of frequency in cycles per time.
• Select Prony if you want Abaqus to calculate the frequency dependence from a time domain Prony series description of the dimensionless shear and bulk relaxation moduli.
• Select Creep test data if you want Abaqus to calculate the parameters in the Prony series from creep test data that you provide. If you select this option, you must enter shear test data and/or volumetric test data in the Test Data Editor.
• Select Relaxation test data if you want Abaqus to calculate the Prony series parameters from relaxation test data. If you select this option, you must enter shear test data and/or volumetric test data in the Test Data Editor.

Read all information about Frequency domain here.

Comparison: Time vs. Frequency Domain

Use Time Domain if:

• You need to simulate long-term deformation (creep in plastics, stress relaxation in rubbers).
• The loading is non-periodic (e.g., step loading, impact).

Use Frequency Domain if:

• The material is subjected to cyclic loading (vibration, noise damping).
• You have experimental DMA data (storage/loss moduli vs. frequency).